14.6 Directional Derivatives and the Gradient

Directional Derivatives

Definition

• We find the derivative of a function of $z=f(x,y)$ in the direction of a vector

  • like looking for the derivative in a certain direction
  • 
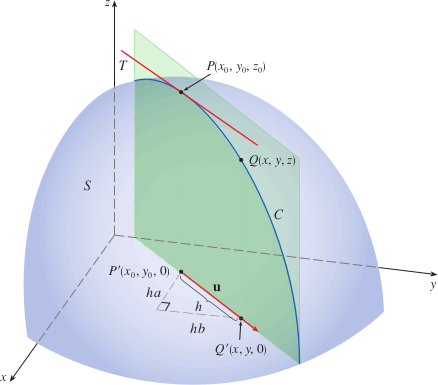
    • so we have the DD as P on the curve of Q in the direction of u

• Theorem

• to find the directional dv given unit vector

$D_u\partial (x,y)={\partial }_x(x,y)a+{\partial }_y(x,y)b$

• When given $\theta$ for the unit vector

$D_u\partial (x,y)={\partial }_x(x,y)\cos \theta +{\partial }_y(x,y)\sin \theta$

The Gradient Vector

Notice!

• That the directional derivative can be writen as a dot product

$D_u\partial (x,y)=<{\partial }_x(x,y),{\partial }_y(x,y)>\cdot u$

• the first vector is extremely useful and is called the gradient of f

The gradient vector

$\nabla f(x,y)=<{\partial }_x(x,y),{\partial }_y(x,y)>$

• this is the gradient of a function, its just the partial of the x y components

Relation between gradient and direction dv

• So since we know the gradient is the first part of the def of ddv

$D_u\partial (x,y)=\nabla \partial (x,y)\cdot u$