What is a projection onto subspaces?
-
Recall 1.5 Projection: we can write x=x1+x2 with x1 parallel to v and x2 perpendicular to v:
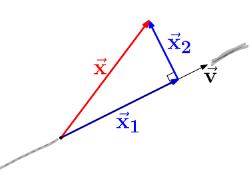
- x1=projv(x)=(∣∣v∣∣2x⋅v)v
- x2=perpv(x)=x−projv(x)
-
In general:
- if W is a subspace of Rn and x∈Rn, we can write x=x1+x2, where x1∈W and x2 is orthoganal to W
-
Simply!
-
We know that x=x1+x2 and each is one another!
- so we can just projw(x)=projv1(x)+projv2(x)
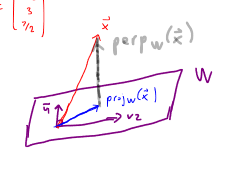
- and to get perpw(x)=x−projw(x)
Orthogonal complement
-
Let W be a subspace of Rn.the orthogoanal complement of W, denoted W⊥, is the set of all vectors that are orthogonal to every vector in W.
- W⊥=(x∈Rn∣x⋅w=0 for all w∈W)
-
If W=span(v1,v2,…,vk),W⊥can be found by writing vi as rows of matrix A, and taking null(A)
Gram-Schmidt process
-
-
The gram-Schmidt process constructs an orthogonal basis (w,…,wk) as follows
-
- w1=v1
-
- let W1=span(w1). set w2=perpw1(v2) (w2 is orthognal to w1)
-
- let W2=span(w1,w2). Set w3=perpw2(v3). (w3 is orthogonal to w1,w2)
-
- proceed in this manner until all w1,…,wk are constructed then w1,…,wk is an orthogonal basis for W
-
notice that we are progressively taking perpendicular parts of vectors before adding them to the new set.

