Assignment 2

Computing Assignment 2 Report

Task 1: Hexagon Creation using Rotation

Given an initial vector ${\vec{v}}_{\text{initial}}=\left(\cos \left(\frac{\pi }{3}\right),\sin \left(\frac{\pi }{3}\right)\right)$, we utilize the rotation matrix to generate a hexagon. The rotation matrix for an angle $\theta$ is defined as:

• $[R(\theta )=\left(\begin{array}{ccc}\cos (\theta )& -\sin (\theta )\sin (\theta )& \cos (\theta )\end{array}\right)]$ To create the hexagon, we rotate ${\vec{v}}_{\text{initial}}$ by $\theta =\frac{\pi }{3}$ radians (60 degrees) five times, appending each result to obtain the vertices of the hexagon.

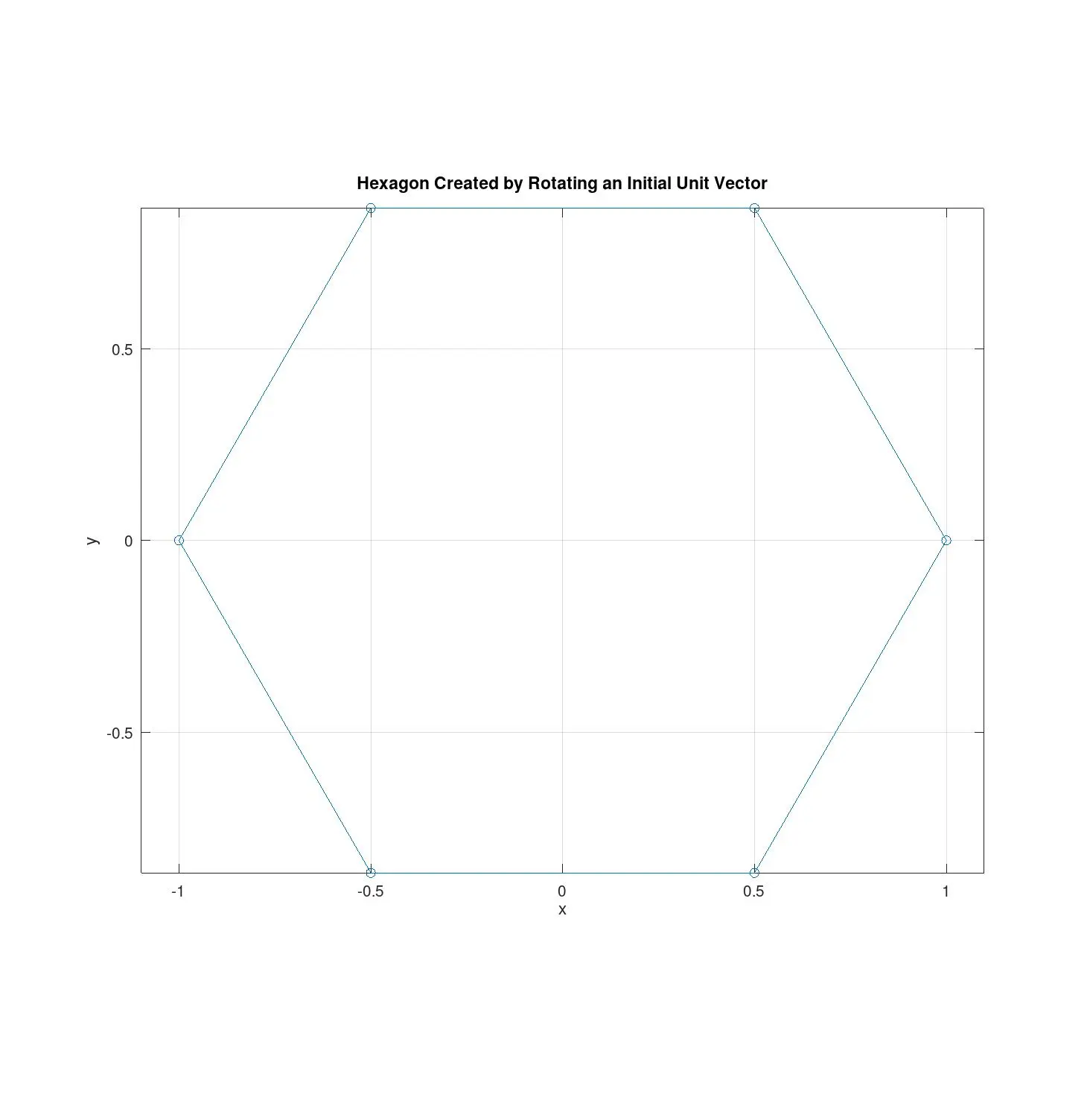
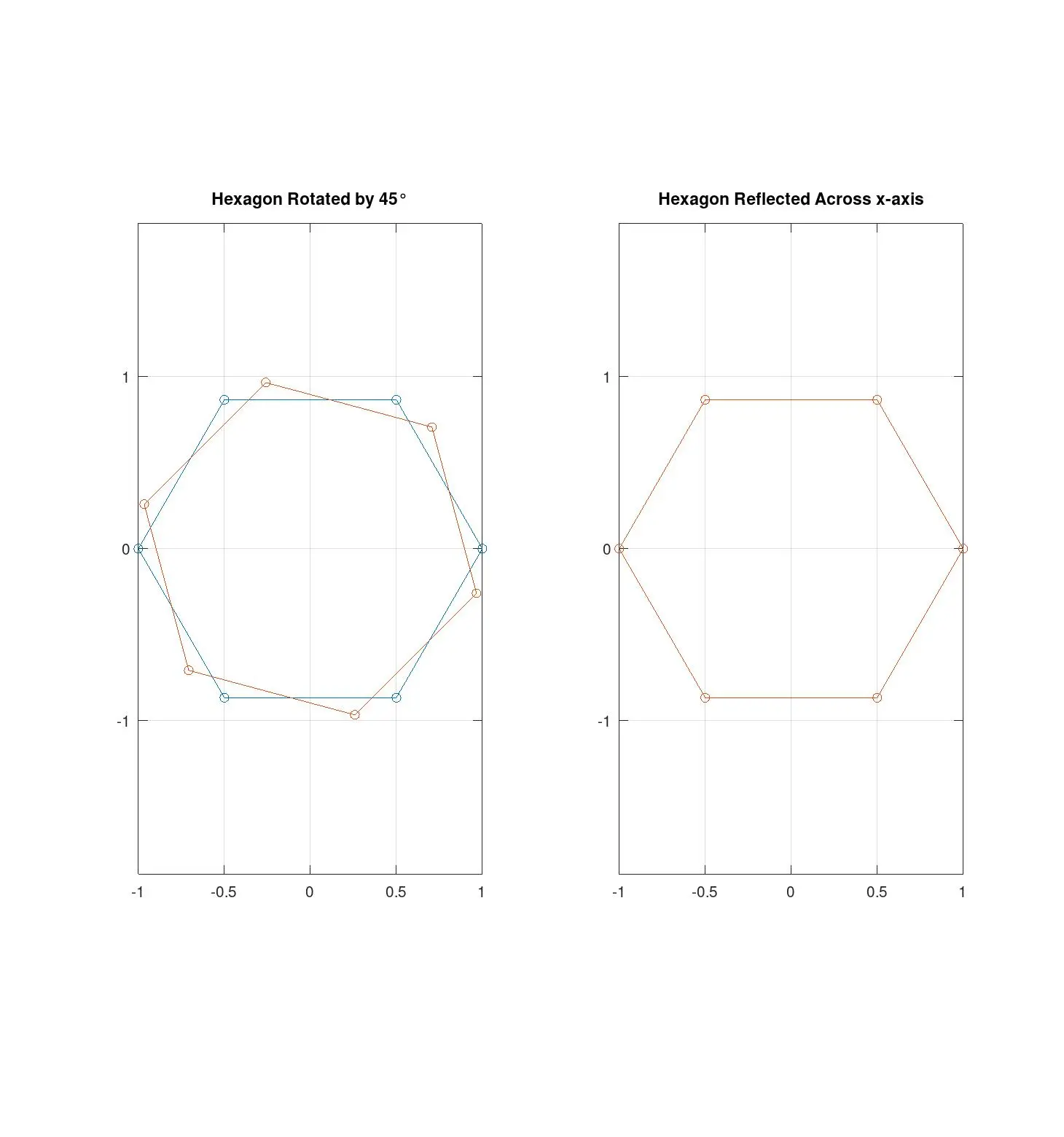
Task 2: Transformations

Two distinct transformations are applied to the hexagon:

1. Rotation by $45^{\circ }$ or $\frac{\pi }{4}$ radians:
   • $[R(\frac{\pi }{4})=\left(\begin{array}{ccc}\cos (\frac{\pi }{4})& -\sin (\frac{\pi }{4})\sin (\frac{\pi }{4})& \cos (\frac{\pi }{4})\end{array}\right)]$
2. Reflection across the x-axis:
   • $[R_{\text{x-reflection}}=\left(\begin{array}{ccc}1& 00& -1\end{array}\right)]$ These transformations are applied to each vertex of the hexagon to generate the modified shapes, showing the effect of rotation and reflection.

Task 3: Composition of Transformations

The commutative property of rotation matrices allows us to combine rotations around different angles ${\theta }_1$ and ${\theta }_2$ in any order, resulting in the same transformation. This is given by the equivalence:

• $[R({\theta }_1)R({\theta }_2)=R({\theta }_2)R({\theta }_1)]$ For non-commutative operations, such as a rotation followed by a reflection, the order matters. This is evident in the difference of outcomes when applying rotation and reflection in opposite sequences:
• $[R_{\text{x-reflection}}R({\theta }_1)\ne R({\theta }_1)R_{\text{x-reflection}}]$