Assignment 3

A16: Car Rental Company

Problem Statement

A car rental company operates at three locations within a city: the airport, the train station, and the city center. The movement of rented cars between these locations follows a certain pattern described by a Markov process with the following transition probabilities:

• From the airport: 80% are returned to the airport, 10% to the train station, and 10% to the city center.
• From the train station: 30% go to the airport, 60% are returned to the train station, and 10% go to the city center.
• From the city center: 30% go to the airport, 10% to the train station, and 60% are returned to the city center.

Objective

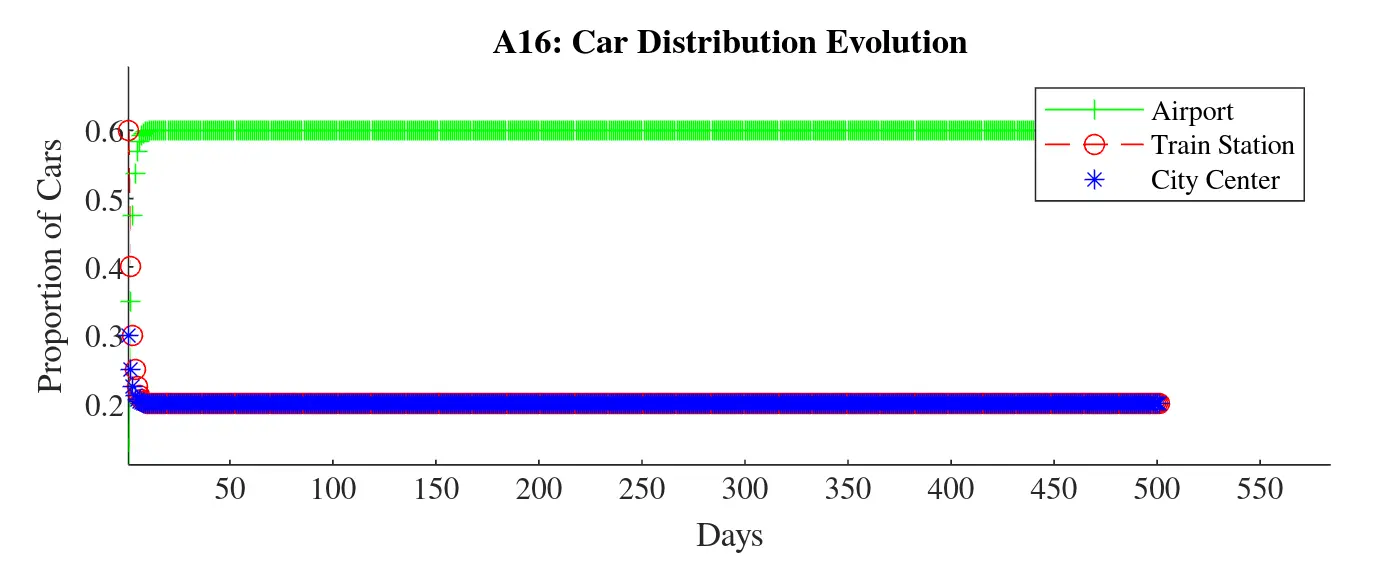
Determine the steady-state distribution of cars among the three locations.

Solution

Let’s denote the steady-state distribution vector as $\mathbf{x}=[x_1,x_2,x_3{]}^T$, where $x_1$, $x_2$, and $x_3$ represent the proportion of cars at the airport, train station, and city center, respectively. Given the transition matrix $P=\left(\begin{array}{ccccccc}0.8& 0.3& 0.30.1& 0.6& 0.10.1& 0.1& 0.6\end{array}\right),$ the steady-state condition can be expressed as $P\mathbf{x}=\mathbf{x}.$ Solving the above condition alongside the normalization condition $x_1+x_2+x_3=1$ leads us to the steady-state distribution vector $\mathbf{x}$.

B15: Bicycle Pool at University Campus

Problem Statement

A student society decides to implement a bicycle pool system with bicycles shared among three locations: the residence, the library, and the athletic center. The daily redistribution of bicycles follows a determined pattern described by a Markov process. Specific daily transitions are given as follows:

• From the residence: 80% stay, 10% go to the library, and 10% to the athletic center.
• From the library: 10% go to the residence, 70% stay, and 20% go to the athletic center.
• From the athletic center: 10% go to the residence, 10% to the library, and 80% stay.

Objective

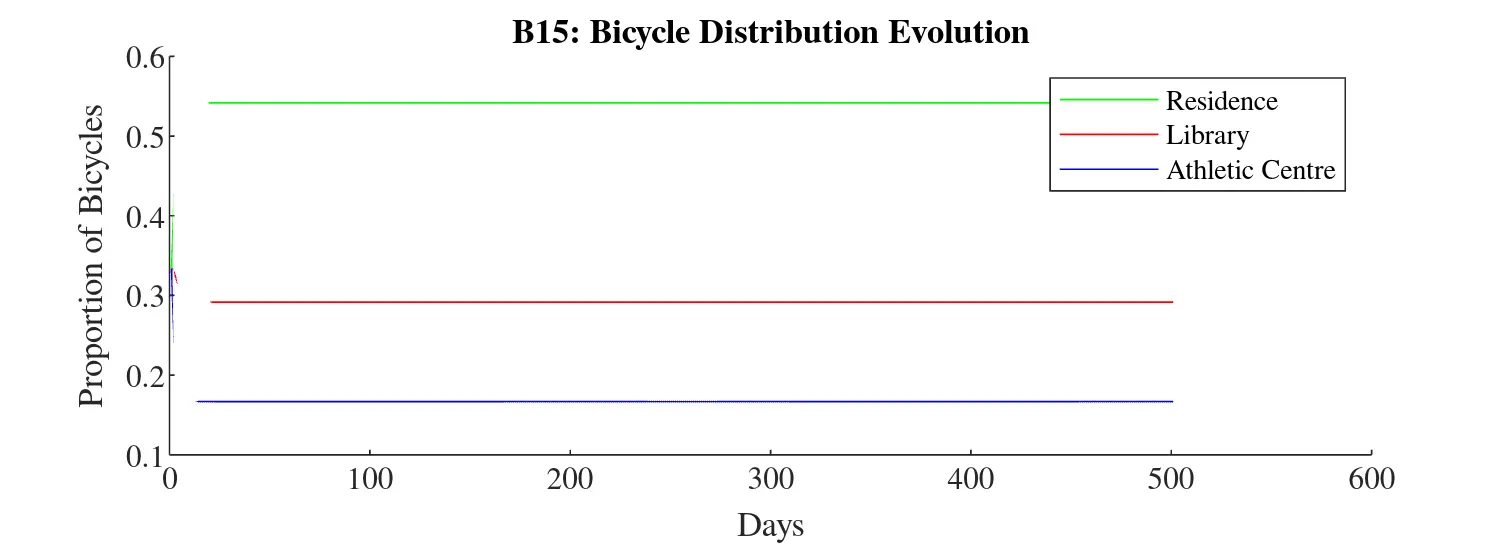
Find the steady-state distribution of bicycles among these three locations.

Solution

Let the steady-state vector be $\mathbf{y}=[y_1,y_2,y_3{]}^T$, where $y_1$, $y_2$, and $y_3$ represent the proportion of bicycles at the residence, library, and athletic center, respectively. Given the transition matrix $Q=\left(\begin{array}{ccccccc}0.8& 0.1& 0.10.1& 0.7& 0.10.1& 0.2& 0.8\end{array}\right),$ the steady-state condition is $Q\mathbf{y}=\mathbf{y}.$ Similar to A16, we solve for $\mathbf{y}$ alongside the normalization condition $y_1+y_2+y_3=1$ to obtain the steady-state distribution of bicycles.

Conclusion

For both A16 and B15, the steady-state distribution is found by solving for the vector that satisfies the equation $M\mathbf{v}=\mathbf{v}$ for matrix $M$ (where $M=P$ for A16 and $M=Q$ for B15), subject to the normalization condition that the elements of $\mathbf{v}$ sum to 1. This demonstrates how Markov processes can model the long-term behavior of systems with transitions between states, ultimately converging to a steady state that does not change with further applications of the transition matrix.