Report

1 Rotation and Reflection of Vectors

Procedure:

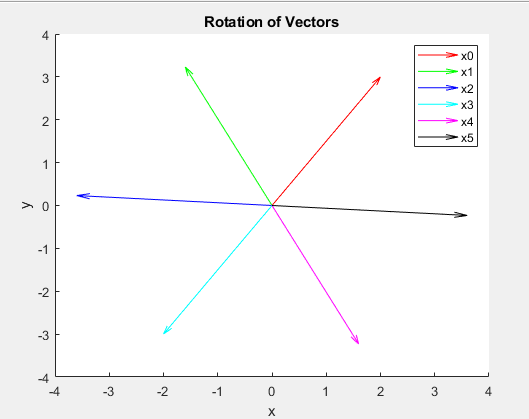
• Rotation:
  • Start with the initial vector $(x_0=\left[\begin{array}{cc}2& 3\end{array}\right]).$
  • Use a $(60^{\circ })$ rotation matrix $(R=\left[\begin{array}{cc}\frac{1}{2}& -\frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& \frac{1}{2}\end{array}\right])$.
  • Compute successive vectors $(x_1,x_2,x_3,x_4,x_5)$ using $(x_i=R\cdot x_{i-1})$.
  • Plot the vectors using different colors.
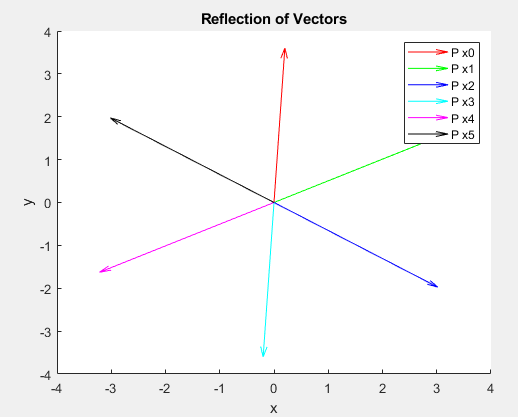
• Reflection:
  • Reflect these vectors over the line ( y = 3x ) using the reflection matrix $(P=\left[\begin{array}{cc}-0.8& 0.6\\ 0.6& 0.8\end{array}\right])$.
  • Compute the reflected vectors$[P]\vec{x}$ for ( i = 0, 1, 2, 3, 4, 5 ).
  • Plot the reflected vectors. Results:

• 1(a) Plot of Rotated Vectors:

  • 
  • $x_n=\left[\begin{array}{ccccc}2.0000& -1.5981& -3.5981& -\mathrm{2.0001.5981}& 3.5981\\ 3.0000& 3.2321& 0.2321& -3.0000-3.2321& -0.2321\end{array}\right]$

• 1(b) Plot of Reflected Vectors:

  • 
  • $[P]x_n=\left[\begin{array}{cccccc}0.2000& 3.2177& 3.0177& -0.2000& -3.2177& -3.0177\\ 3.6000& 1.6268& -1.9732& -3.6000& -1.6268& 1.9732\end{array}\right]$

---

2 Basis Transformation and Linear Mapping

Problem Statement: Given basis $(B=v_1,v_2,v_3,v_4):[v_1=\left[\begin{array}{c}0121\end{array}\right],v_2=\left[\begin{array}{c}1501\end{array}\right],v_3=\left[\begin{array}{c}2364\end{array}\right],v_4=\left[\begin{array}{c}13-1-1\end{array}\right]]$ Procedure:

• Compute the basis transformation matrix ( P_{S \to B} ).
• Given the vector $(x=\left[\begin{array}{c}1234\end{array}\right])$, compute its representation in basis ( B ).
• Define the linear transformation: $[L(x_1,x_2,x_3,x_4)=\left[\begin{array}{c}{x}_2+5x_4{x}_1-x_3{x}_1+x_2+x_3+x_{4}0\end{array}\right]]$
• Compute the matrix representation of ( L ) in the basis ( B ) and use it to find $((L(x){)}_B)$.

Results:

• Transformation Matrix $(P_{S\to B})$:

$$PS\to B:\left[\begin{array}{cccc}-1.1481& 0.3704& 0.6667& -0.7037\\ -0.2593& 0.1481& -0.3333& 0.5185\\ 0.4444& -0.1111& 0.0000& 0.1111\\ 0.3704& 0.0741& 0.3333& -0.7407\end{array}\right]$$

• Coordinates of x in basis B:

$$x_B=\left[\begin{array}{c}-1.2222\\ 1.1111\\ 0.6667\\ -1.4444\end{array}\right]$$

• Matrix Representation of ( L ) in Basis ( B ):

-4.9630 & -6.4444 & -17.8889 & 4.3704\\ -3.1852 & -4.7778 & -11.5556 & 0.1481\\ 2.8889 & 4.3333 & 10.6667 & -1.1111\\ 3.4074 & 6.1111 & 13.2222 & 0.0741 \end{bmatrix}$$ - **Transformed Vector $( (L(x))_B )$**:

\tiny Lx_{b}= \begin{bmatrix} -19.3333\ -9.3333\ 10.0000\ 11.3333\ \end{bmatrix}