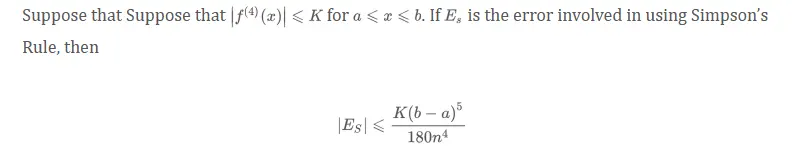Approximate Integration

Unit 7.7 of Math 152

Motivating problem: Evaluate ${\int }_0^1{e}^{-x^2}dx$

• No elementary antiderivative

  • very hard :(
    • but we can approxomate it by doing riemann sums
      • Riemann sums are ineffictiant and inaccurate! so we use a new way that is simmilar to mid point rule and riemann sums

        • Trapazoidal rule!

trapazoidal rule

• The trapazoidal rule is defined by

    - $\int _{a}^{b}f(x)\approx \frac{\Delta x}{2}[f(x_{0})+2f(x_{1})+2f(x_{2})+\dots+2f(x_{n-1})+f(x_{n})] \, dx$
    	-  *where* $\Delta x=\frac{b-a}{n}$ 
    	- Its kinda like a sandwhich on the ones that are multiplied by 2
  

• Error bounds for Trapezoidal rules

  • What error is definded by is

    • 

  • Error bounds is calculated by

  • 

    • This only calculates the MAX error not the exact

Simpsons rule :)

• The simpsons rule is definded by

  • ${\int }_a^{b}f(x)\approx \frac{\Delta x}{3}[f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+\cdots +2f(x_{n-1})+f(x_n)]dx$
    • Basicly we are just turning the linear function from the trapazoidal rule into a quadratic, kinda like a spline

• Error bound for simpsons rule

  • Error bounds are calculated by

    •