Assignment 1

Part 1: Solutions of Systems of Linear Equations

---

Code Components

• Entry Function (part1): Initiates analysis for three cases by specifying (m) and varying (n).
• Independence Test Function (test_linear_independence): Assesses independence through trials using:
  • Random Matrix Generation: Y = randn(m, n) produces matrices (Y) to represent sets of vectors.
  • Rank and Pivot Analysis: Computes the matrix rank (rank(Y)) and pivot positions from the row-reduced echelon form (rref(Y)), crucial for determining vector independence.

Why It Works

• Empirical Approach: Repeatedly testing with random matrices statistically samples vector sets under specific dimensional conditions, providing practical insights into theoretical expectations of linear independence.
• Linear Algebra Principles: Utilizing matrix rank and echelon form as indicators, the code applies well-established criteria for independence. A matrix’s full rank equal to (n) and matching pivot positions signify linear independence among vectors.

Rationale

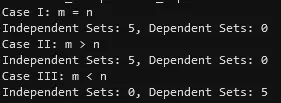
• Scenario Exploration: By evaluating (m = n), (m > n), and (m < n), the code comprehensively examines potential outcomes for vector sets, reflecting how dimensional relationships influence linear independence.
• Statistical Validation: Through numerous trials, the approach allows for observing the likelihood of independence or dependence in varied setups, highlighting the interplay between dimensions and vectors.

Output:

Part 2: Linear Independence & Intersection of Subspaces

Objective:

To determine the inclusion of vectors (z_2) and (z_3) in the subspace (S_1), defined by specific basis vectors.

Approach:

• Basis vectors of (S_1) were identified and compiled into matrix (A).
• Vectors (z_2) and (z_3) were assessed for linear representability in terms of (A)‘s columns.
• Solutions for (Ax = z_2) and (Ax = z_3) were sought, with residuals used to verify accuracy.

Key Findings:

• Matrix (A) accurately represents (S_1) using chosen basis vectors.
• Systems were solved to identify if (z_2) and (z_3) can be expressed as linear combinations of basis vectors in (S_1).
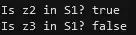
• Residual Analysis showed that both vectors have their presence evaluated against a predetermined tolerance to determine their inclusion.

Output:

Conclusion:

(z_2) and (z_3) resides within (S_1) by examining their expressibility as linear combinations of (S_1)‘s basis and analyzing the solution residuals against a tolerance level. The concise analysis rendered a definitive stance on the vectors’ membership, providing insights into (S_1)‘s characteristics relative to (z_2) and (z_3).