Definition
-
A vector is a quantity with both a magnitude and a direction
-
not to be confused with scalar that is only a magnitude
Representations of a vector
-
A vector v can be denoted by an arrow in Rn, but we must denote its length as ∣v∣ (to show its direction and magnitude)
-
vectors can be represented any where as long (we usually use the origin because its easy)
-
In R2 its called an ordered pair
-
in R3 its called a ordered triple
-
vectors in R2,R3
-
v=(a,b),R2
-
v=(a,b,c),R3
- these numbers a b c are called components of the vector
- the length of v can be found as just using Pythagoras
-
position vector:
-
The vector v is called the position vector of the point
Special vectors
-
The 0
-
it is special because it has no direction
-
Unit vector
-
standard basis vectors
- i^=(0,0,1),j^=(0,1,0),k^=(1,0,0)
Algebraic operations with vectors:
-
Addition:
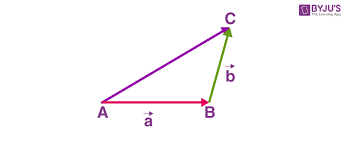
- u+v=(u1+v1)+(u2+v2)+(u3+v3)…(un+vn)
- geometrically its just the A→C line
-
Scalar multiplication
- if c is a real number you can just extrude the vector
-
Difference
- u−v=u+(−v)
- geometrically its similar to addition but we put the 2 initial positions together instead of stacking them
Examples
How to find all possible values of a variable to be a unit vector
-
find all possible values of α to make u=(41,−21,α)
∣u∣2=1(41)2+(−21)+α2=1