12.1 Three-Dimensional Coordinate System

Summary

• 3d Coordinate system and sketch:

  • points
  • surfaces
  • curves
  • regions

    • Geometry is a centerpiece of this course

    • Sketching is a required skill and will be tested throughout this course

Review

• Recall the 2D coordinate system

  • We must be consistent in our graphs image
    • We can rotate the graph

      • But we cant mirror it! (you could but you need to be consistent)

  • We can add a 3rd dimension by adding a line coming out of the intersection of the x-y plane

• Right hand rule

  • 
    • where we curve our hands towards the y-axis

• Coordinates planes

  • We know the xy plane, but we can do this for all permutations of the varibles

    • X-Y Plane

    • X-Z Plane

    • Y-Z Plane

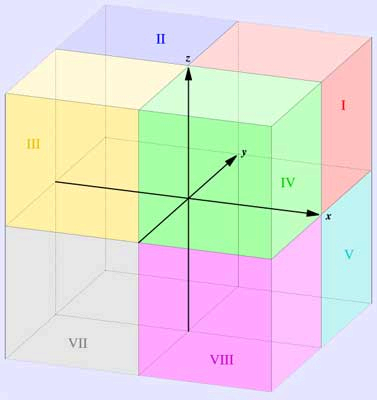
  • Because of this we have octants like the quadrants of a 2d plane

    • 

Coordinate systems in ${\mathbb{R}}^3$

• It is simple it follows (x,y,z)

  • this is self explanatory…

• Projection of points to coordinate planes and axes.

  • If we are projecting onto a plane such as the xy plane we just take the xy coordinates and throwaway the rest

    • this is similar to 1.5 Projection
    • note we dont get rid of the redundant coordinate we just enter a 0

Sketching in ${\mathbb{R}}^3$

• if its a 2 varible function we can just sketch it but we need to extrude in the direction of the free varible

  • Because the 3rd varible is a free varible so any value still would satisfy

• EX.

  • $y^2+z^2=4$

Distance formula

• The distance between two points $P_1(x,y,z)$ and $P_2(x,y,z)$ is

  • $\mid P_1{P}_2|=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2}$
    • this is derived because each point is perpidicular to each axis so they are sqares, we can just find the hypotunes